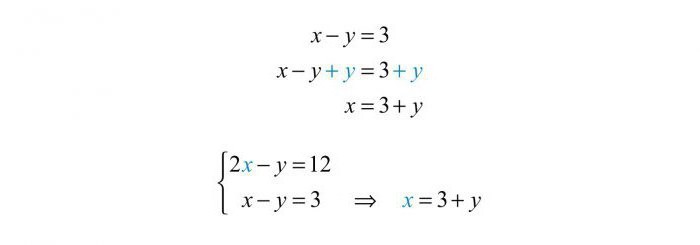מטריצה מתמטית. כפל של מטריצות
עדיין מתמטיקאים של סין העתיקה בשימושרישום החישובים שלהם בצורה של טבלאות עם מספר מסוים של שורות ועמודות. אז אובייקטים מתמטיים דומים נקראו כמו "ריבועים קסם". אמנם יש מקרים ידועים של שימוש בטבלאות בצורת משולשים, אשר לא נעשה שימוש נרחב.
עד כה, תחת המטריצה המתמטיתנהוג להבין את נפח צורת מלבני עם מספר נתון של עמודות וסמלים, אשר קובעים את הממדים של המטריצה. במתמטיקה, צורת כתיבה זו מצאה יישום רחב עבור ההקלטה בצורת קומפקטית של מערכות של משוואות אלגנטיות, ליניאריות, אלגבריות. ההנחה היא שמספר השורות במטריצה שווה למספר המשוואות הנמצאות במערכת, מספר העמודות מתאים לכמות הבלתי ידועים שיש לקבוע במהלך הפתרון של המערכת.
בנוסף, כי המטריצה עצמה במהלך שלהפתרון מוביל למציאת הבלתי ידוע המשובץ במצב של מערכת המשוואות, ישנם מספר פעולות אלגבריות שניתן לבצע על אובייקט מתמטי זה. רשימה זו כוללת תוספת של מטריצות בעלות אותם מימדים. הכפלה של מטריצות עם מידות מתאימות (ניתן להכפיל רק את המטריצה, מצד אחד יש מספר עמודות השוות למספר השורות של המטריצה בצד השני). ניתן גם להכפיל את המטריצה על ידי וקטור, או אלמנט של השדה או את טבעת הבסיס (אחרת הסקלר).
בהתחשב בכפל של מטריצות, זה נובע מכךבזהירות לפקח על מספר העמודות של הראשון בהחלט מקביל למספר שורות של השני. אחרת, פעולה זו על המטריצות לא תיקבע. על פי הכלל שעליו מטריצה המטריצה מטריצה, כל רכיב במטריצה החדשה משויך לסכום המוצרים של האלמנטים המתאימים משורות המטריצה הראשונה לאלמנטים שנלקחו מעמודות האחרת.
לשם הבהירות, הבה נבחן דוגמה לאופן שבו מתרחשת הכפל של המטריצה. אנחנו לוקחים את המטריצה א
2 3 -2
3 4 0
-1 2 -2,
להכפיל את זה על ידי מטריצה ב
3 -2
1 0
4 -3.
אלמנט השורה הראשונה של העמודה הראשונההמטריצה המתקבלת היא 2 * 3 + 3 * 1 + (-2) * 4. בהתאם לכך, בשורה הראשונה בעמודה השנייה יהיה אלמנט השווה ל -2 * (-2) + 3 * 0 + (-2) * (-3), וכך הלאה עד שכל רכיב של המטריצה החדשה יתמלא. הכלל למכפילים מתרבים מניח שהתוצאה של תוצר של מטריצה עם פרמטרים m x n על מטריצה בעלת היחס n x k היא טבלה בעלת מידות m x k. בעקבות כלל זה, אנו יכולים להסיק כי המוצר של מה שנקרא מטריצות מרובע, בהתאמה, מאותו סדר מוגדר תמיד.
מן המאפיינים שיש כפל מטריקס,זה צריך להיעשות כאחד העובדה הבסיסית כי פעולה זו אינה קומוטטיבית. זהו התוצר של M מטריקס ל- N הוא לא שווה למכפלה של N ידי M. אם מטריצות מרובעות מאותו הסדר הוא ציין כי המוצר קדימה הפוך שלהם נקבע תמיד, והן נבדל רק התוצאה, המטריצה המלבנית כמו תנאים מסוימים אינן מתקיימת תמיד.
כפל של מטריצות יש מספר מאפיינים,אשר יש הוכחות מתמטיות ברורות. הכפלה אסוציאטיבית אומרת נאמנות הבאות לביטוי מתמטי: (MN) K = M (נ"ח), שבו M, N, ו- K - מטריצה שיש את הפרמטרים שבם כפל מוגדר. כפל Distributivity מניחה M (N + K) = MN + ח"כ, (M + N) K = ח"כ + NK, L (MN) = (LM) N + M (LN), שבו L - מספר.
תוצאה של תכונה כפל מטריצה, המכונה "אסוציאטיביות", מרמז כי עבודה המכילה שלושה גורמים או יותר מותר לכתוב ללא שימוש בסוגריים.
שימוש במאפיין ההפצה מאפשר לפתוח סוגריים בעת בחינת ביטויים של מטריצות. אנחנו שמים לב, אם אנחנו פותחים סוגריים, אז אנחנו צריכים לשמור על הסדר של הגורמים.
השימוש בביטויים מטריקס מאפשר לא רק להקליט קומפקטית מערכות מסורבל של משוואות, אלא גם מקלה על תהליך העיבוד שלהם ופתרון.
</ p>